Pinhole cameras generally need significant vignetting correction. They tend to have very wide angles of view, which means that the corners of the frame are much further from the pinhole than the center. Light falls off with the inverse square of the distance form the source; a common pinhole camera that has a frame three times as wide as its focal length will have about two stops of falloff at the corners (that is, the corners receive 1/4 as much light as the center). The formula is falloff = ((d/ƒ)^2, where d is the distance from image center and ƒ is the focal length of the camera.
I've written a tool to generate Adobe Lens Profiles to correct for this in Adobe Camera Raw and Lightroom:
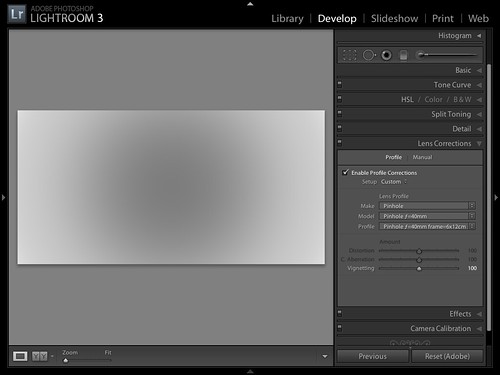
... but due to the way Adobe's lens profiles are implemented, they are far from perfect. You can't separate the X axis from the Y (as you'd need to do for the curved film plane cameras discussed in the other thread), and they approximate the falloff using a limited 6th degree polynomial but using only the coefficients for the 2nd, 4th, and 6th terms, which approximates the actual curve poorly in many cases, as seen in the graphs in this feedback to Adobe.
While I know this correction can likely already be done in ImageMagick using maps, because the math is so simple it would be great to be able to do this in a straightforward way on the command line without going through that process. The user would only need to specify the frame/focal-length ratio in both the X and Y axes, then you calculate the falloff and correct algorithmically.
Is this already doable in a straightforward way? If not, can I beg for a command-line implementation? If so, then for pinhole photographers it becomes a simple pass through ImageMagick for vignetting and distortion correction before importing into Lightroom or Photoshop.
Thanks for considering this!







