ImageMagick v6 Examples --
Color Basics and Channels

Index

ImageMagick Examples Preface and Index

What is to Color

• What is Color?
• RGB color space
• CMY color space
• CMYK color space
• Other Color Spaces

Human Color Perception

• Gamma Correction
• sRGB Colorspace Correction
• Gamma of your Monitor
• Processing Real Images

Color Channels

• ColorSpace - How Color is Stored
• Separating Channel Images
• Grayscale Channels from Colorspaces
• Other Channel Separation Methods
• Combining RGB Channel Images
• Combining non-RGB Channel Images
• Generating a ColorWheel
• Zeroing Color Channels

Color Specification

• Colors by Name
• Color Name Conflicts
• Semi-Transparent Colors

Replacing Colors in an Image (replacing specific colors)

• Replace a Specific Color
• Replace a Color in the Image
• Floodfill Draw
• Floodfill Operator
• Fuzz Factor, Matching Near Colors
• Fuzz Factor Distance
• Fuzz Factor and Transparent Colors

Raster Images, which is what ImageMagick deals with (in general) basically consists of an array of individual points or pixels of color. Modifying the individual points and how they are represented is what we will look at in this section.

In the next section we will look at more general global modification of the colors in an image as a whole.

---

What is Color?

To really understand color, you need to know exactly what color is.

In the physical world color is actually an illusion. We see color because our eyes sense the physical world in very special limited way. Basically in our eyes we have special sensors for Red, Green, Blue, and a minor lesser sensor for peripheral and low light conditions. The later is why we see only grey colors at night.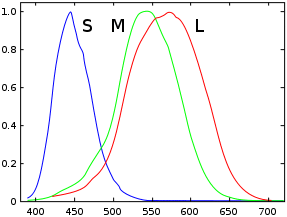

For more info see Wikipedia, Cone Cells, the graph right which is the response of a typical human eye to different wavelengths of light.

Because of this we only sense the world in terms of Red, Green and Blue electromagnetic wave lengths, and this is why images and image processing is generally all about Red, Green, and Blue, or RGB.

However it isn't quite as simple as that either. Each of our color sensors actually respond to a range of wavelengths. For example when we see a yellow light, we actually sense the light using both red and green sensors. If our color sensors were strictly pure red and green, we would not see any yellow colors at all.

That means a TV or computer display is actually fooling us into seeing yellow by the monitor emitting just the right mix of red and green light, rather than actual yellow light. Our color sensors see the same intensity as it would for a pure yellow light, and as a result we see yellow, even though in reality we are really seeing two different color frequencies. We just can not tell the difference between a pure yellow, and a mix of red and green light.

ASIDE: Other animals have slightly different sensors to us. Bees and most other insects have sensors for ultra violet, as such to them our printed images, TVs, and billboards would probably make very little sense to them. More than likely these artificial images would probably look more like rather than horrible false color image rather than the near perfect color we are being fooled into seeing. Some animals have 4 color sensors, while others only have one (black and white) or two. Also some animals see movement far better than any specific color (such as a bull, who contrary to popular beliaf can not see red, only black and white), as such a monitor may appear to be a blaze of movement due to the 50/60Hz update cycle.

For more information see Wikipedia, Color Vision and Wikipedia, Color.

RGB Color Space, and Channels

So RGB color space is really a way of representing images using three values Red, Green, and Blue, that will fool us into thinking we are seeing something in the real world. Images can thus be stored as an 3 arrays values, with each of the three values forming a single pixel, or point of color, to be displayed.

Each of the three arrays of values are known as a channel, which is simply a gray-scale image representing the amount of light to create for just one of our color sensors.

For example here are the red, green, and blue components of a rose image.

Rose

Red

Green

Blue

Note how the 'Red' image is much brighter to display a rose, than the other two color components. But all three images are bright for the white patch near the bottom.

RGB are Additive Colors

Now Red, Green, and Blue colors are termed 'additive' colors. That is the colors are added together to form the final color image. This is because those are the dominant colors our eyes see, and by combining them together we can effectively generate almost every color our eyes can see.

They are additive in that starting with black, such as a blank monitor, you would then add red, green, and blue light to generate the appropriate colors for the image we see. The key to this is that you start with a black, or the absence of light, and then add appropriate amounts of red, green, and blue.

You can also get the same effect by shining three torches with red, green and blue cellophane taped over the ends, in a dark room. When the three colors shine on the same spot say on a white wall, we see white.

It is because of how our eyes actually see these 'primary' colors, that color images are generally expressed in terms of RGB values, which are also termed 'color channels'.

CMY color space

When you are printing you have a different problem. A piece of paper can not generate light, only reflect it. As such you need to start with a surface that reflects all the light that hits it, in all directions. That is what a white surface is. Hopefully the light it is reflecting is itself a pure white light either from the sun shining in the window, or being generated by the lights in our artificially lit rooms.

Now to create an image on that paper you need to apply ink to that surface, which actually removes particular wavelengths of light. As we 'sense' red, green, and blue colors, those are the colors we want to selectively remove from the light reflecting from that white piece of paper. Consequently we use a cyan ink to remove red light, magenta to remove green light, and yellow to remove blue light. The amount of Cyan, Magenta, and Yellow ink needed to generate a specific color produces what is termed CMY colorspace.

Here I generate a ink masks is needed to generate a rose image using just cyan, magenta and yellow inks (assuming the inks are 'linear')

Rose

Cyan

Magenta

Yellow

That is the brighter the cyan mask values, the more cyan ink will be needed to remove more of the red. In other words a cyan mask is the exact negative of the mount of red light we want the paper to reflect.

In fact all three of the above channel images are the exact negative of what was generated for RGB color-space.

So really to convert a RGB image to a CMK image all that you need to do is Negate the Image and then declare the image to be in CMY color-space.

As we are selectively removing wavelengths, Cyan, magenta, and Yellow are known as 'subtractive colors'.

CMYK color space

The major problem with selectively removing wavelengths, is that just removing all red, green, and blue light, by applying all three cyan, magenta, and yellow inks, does not actually remove all the light that is being reflected. As a result you will be left not with a black color, but a horrible looking muddy brown color.

The inks (or light filters) are not perfect, just as our own eyes are not perfect. As I mentioned before, each of our color sensors does not see just one wavelength of light, but a range of wavelengths that we interpret as being 'red' 'green' or 'blue' (or a mix of those colors). So much so that our 'blue' light sensor can actually see (though not very well) a little ultra violet, which is why we can just sense 'black light lamps' in a perfectly dark room.

It is because of this 'leakage' of color from the CMY inks, and our own imperfect eyes, that we also add a pure black ink to the mix, allowing it to be used to wipe out ALL light that could be reflected from paper. To prevent it being confused with blue the black ink or channel is assigned the letter K. As such for printing we use four colored inks: Cyan, Magenta, Yellow, and blacK; and define images using these inks, to form a CMYK color space.

For example here are the appropriate CMYK components separated out from this image.

Rose

Cyan

Magenta

Yellow

blacK

Note how the amount of cyan, magenta, and yellow has been reduced and is now darker than in CMY colorspace, as there use was replaced by an appropriate amount of black. That is when all three inks are present for a particular pixel, black is used instead. As such to print say pure black, you only use pure black ink, and no other inks.

Remember the 'blacK' in the above is the amount of black ink to apply to a piece of paper, so the brighter the greyscale channel image is, the more black ink should be used. As such it is also a negative looking image, just like the other three images.

Of course adding a pure black in a color printer makes printing black text, a lot simpler, as you no longer need to print three different inks, overlaid perfectly on the same spot, to generate pure black lines, letters, and shapes. This means far less ink, with the paper becoming less 'wet' and less likely to run or smuge, which is especially good for printers.

For another similar discussion of how RGB and CMYK colors work see the introduction page of. XaraXone Workbook, Defining Color.

Other Color Spaces

Other colorspaces are just other ways of representing those same colors, or some of the others beyond strict RGB that our imperfect eyes can also make out. However such color spaces have little bearing on either displaying those colors using a monitor, or in printing.

They basically represent other ways of of representing and/or processing of image, so as to enhance or highlight things such as...

• Better non-linear handling of Dark Colors (sRGB)
• Color rainbows and hues (HSB, HSL color spaces)
• Standardized definition colors (XYZ)
• Precise Color Difference (LAB colorspace)
• Better compression of color values (such as in YIQ and YUV)
• Transmission for TVs (YCbCr, YPbPr, where Y = BW signal)

One final colorspace I have yet to mention is 'Gray-Scale', but that is just a simple single array of pixel values. IM actually does not have such a color space, and only fakes, it with RGB color space, setting all RGB settings to the same value. If the three values are not the same, the image is no longer grayscale.

For more information on different color space representations see Wikipedia, RGB color model, sRGB variant, CMYK, HSL and HSV (HSB), YIQ, YUV, L^*A^*B^*, XYZ.

The above changes to the 'colorspace' of an image is only a gross arrangement of the colors of an image within memory. It also provides very basic (simplistic) color conversions between different colorspaces. For exact color specifications and color conversions Color Profiles should be used instead, but only works when using image file formats that can handle color profiles.

---

Gamma Correction and sRGB Colorspace

Human Color Perception

In the above we saw that you can represent images in many different ways. All the color-spaces we looked at above are known as 'linear' colorspaces, which means that the actual value used represents the actual 'intensity' values of the color in an image.

However real life is never quite so simple. For example lets generate and save an image of a simple linear gradient. As per the Gradients of Color. convert -size 100x100 gradient: gradient.gif

Now the actual color values used in this image are a linear gradient that should smoothly change from white at the top to black at the bottom. However if you look at the image you will see that the image actually seems to contain a lot more dark (near black) colors than light (near white) colors.

Why? Well human vision when given a light intensity that is only half of its maximum range ('white') does not see the pure mid-tone grey that the color value indicates, but a much darker color. As a result the above linear gradient does not look like a uniform linear spread of colors from white to black, but has far more darker colors than it should.

The actual image value to perceived value is roughly a 'power function' of the form...

The value '2.2' is the average gamma function value, typical of most human beings.

Gamma Correction

Gamma Correction is a way of adjusting the color values that are actually saved, so that the final image looks much more uniform in its spread of colors.

Basically while human vision makes light look darker using a power factor of 2.2, to make a linear image 'look' linear we need to reverse that power function, using a value of 1/2.2. That is to make an image look linear, we need to correct it using the following formula...

IM provides Gamma correction via either the Level Operator, Gamma Argument, or more specifically using the Gamma Operator. However you could also directly modify the image values using the Evaluate POW function.

So lets apply it and see the result of a 'gamma corrected image'.. convert -size 100x100 gradient: -gamma 2.2 gradient_gamma.gif

Note how the image now has far more equal amounts of light and dark colors. However the actual values within the image is no longer 'linear', which can cause problems when processing this image later.

Gamma correction is only a rough 'quick' method of adjusting the colors to make an image. However it is not the usual method of correcting a image for human response.

sRGB Colorspace Correction

Saving an image using a sRGB Colorspace is very similar to Gamma correcting an image, but is slightly more complicated so as to better reproduce the actual response of the human eye, specifically with very dark shades of color.

So lets save our linear gradient in a sRGB corrected colorspace. convert -size 100x100 gradient: \ -set colorspace sRGB -colorspace RGB gradient_sRGB.gif

Though even this is not actually a perfect representation. In fact a perfect represntation is impossible as no two individuals are exactly the same. Simply put: what you see, is never exactly what other people see (very Zen). All it is, is a very good approximation for the majority people, according to numerious surveys, color printers, and color experts.

For details of the exact sRGB formula see Wikipedia, sRGB Colorspace.

The World Wide Web has standardized on the use of sRGB as the recommended default color space, and should thus be used for all images that do not contain any colorspace profile information. That is for images such as GIF, PNG, JPEG and TIFF.

The way IMv6 handles 'sRGB' colorspace is actually reversed. That is to say specifying "-colorspace sRGB" converts a image from sRGB to RGB, and visa-versa. That is "-colorspace sRGB" actually converts an image from sRGB to linear RGB colorspace. This was the result of IM choosing RGB as its internal default, rather that the network default of sRGB. This colorspace handling weirdness is considered a bug, and is one aspect that will be fixed as part of the planned IMv7 development. However it will not be fixed in IMv6.

And here are all three images together so you can compare them.

Linear	Gamma	sRGB

As you can see Gamma and sRGB corrected images are nearly identical, and the difference when graphed is actually extremely minor. As such while using sRGB is the more correct method, using Gamma Correction is probably easier to apply.

Gamma of your Monitor Stand back from your monitor a few meters (yards) and look at the image to the left. If your monitor (and web browser) is displaying the sRGB image correctly, the point where the central 'hash' pattern is about equal brightness to the surrounding sRGB gradient should be in the very middle. Most computer monitors fail this test! However HDMI TV's should come out perfect. The image was created using... convert -size 45x256 gradient: -size 10x256 pattern:gray50 \ -duplicate 1,0 +append -set colorspace sRGB -colorspace RGB \ monitor_sRGB.png

Here are some similar images with differnent 'gamma' levels so you can see how close your monitor is to a correct '2.2' gamma display for human perception.

The image that (when you stand back) where the point of equal brightness is about the 50% mark, tells you about the rough gamma level of your monitor. If properly tuned, your monitor should have a gamma level of 2.2 which very closely matches that of sRGB colorspace.

My current work monitor (a LCD that is a few years old) is very poor and displays images with a gamma of only 1.8. Hopefully my replacement monitor will be a lot better!

Processing Real Images

Most image processing operators do not care what colorspace an image is using, it just applies its operations to the channel data regardless of its colorspace. Though some have to make special effort for handling the extra channel data for 'Black', and as you will see later 'Matte' (or inverted 'Alpha' transparency).

However the colorspace of an image can greatly influence the final result of many operations. As such doing image processing in a different color space can generate improved results than if you directly applied the operation in the normal RGB colorspace. This is especially true of Color Quantization (color reduction), but also in Image Resizing and more generatally Image Distorting.

Cristy, the ImageMagick Coordinator, recommends 'YIQ' colorspace for color quantization. Basically as this color space emphasizes mid-tones and pastel colors, whcih is more suitable for skin-tones, rather than the less common primary colors. This is espeically usefule for GIF and palette PNG images, used for generating image thumbnails. Helmut Dersch (of Barrel Distortion and Len Correction fame) recommends that you should consider using the linear 'LAB' colorspace for processing image especially distortions. I only recommend that you move from the 'input' sRGB colorspace to some other 'linear' colorspace, when doing drawing, compositions, resizing or distortions of images. Whether this is linear-RGB or LAB should not matter that much.

For examples of processing images with reagrd to colorspace see Resizing with Colorspace Correction.

Also see warnings about colornames and drawing in linear colorspace, in Drawing with Gamma and Colorspace Correction

---

Color Channels

The actual color data of an image is stored as arrays of values, known as channels. Typically an image will have at least 3 channels, representing red, green, and blue color values. But as you saw above the values stored could represent other colorspaces.

Colorspace, and Channel Naming

The primary purpose of "-colorspace" operator is to change the way IM stores the colors of an image within memory.

Normally each image has 3 (or 4) channels of image data. The current 'color space' of an image determines what the data of each channel represents. Now normally the channels are named 'Red', 'Green', 'Blue', as that is normally the type of image data that is stored in those channels. However that is not always the case.

Don't think of the 'R' or 'Red' channel as being red, think of it as 'channel 1' which could contain data for 'red', 'hue', 'cyan', or other things depending on the colorspace of the the image. 'Red' is just a label for the channel typically used for 'red', or the first channel.

The second most common colorspace used is 'CMYK', which defines the amount of color 'ink' that should be applied to a darken a 'white' piece of paper (a subtractive colorspace). Note that K is short for "blacK", which a negated intensity values of the image.

As this is very common the 'RGB' channels also have an alternative naming of 'Cyan', 'Magenta', and 'Yellow', or just the letters 'C', 'M' and 'Y', though in reality they refer to the same set of channels that is used for 'RGB' images. A special fourth color channel is also added for the 'Black' or 'K' color channel.

This basically means that the color channel for "Green" actually refers to the exact same color channel as would be used for "Magenta". Whether the data itself is 'green' or 'magenta' depends NOT on the name of the channel, but the 'colorspace' of the image in memory.

The same thing happens for other colorspaces. For example using a 'LAB' color space means the 'Red' channel contains the 'Lightness' value, while 'Green' channel holds the 'A' (or red-green) value, and 'Blue' channel holds the 'B' (or blue-yellow) value.

In a similar way, the channel names 'Alpha' ('A'), 'Opacity' ('O'), and 'Matte', are all aliases for the "-channel" setting referring to the images transparency information. It does not matter that an 'alpha' channel is the inverse of a 'matte' channel, it still refers to the same channel, and produces the same result, the Internal Matte Channel of the image.

Whether an operator treates the internal matte channel data as a 'matte' or and 'alpha' value depends of the operator. Low level channel operators like "-threshold" work on the raw 'matte' data of the channel in memory. However most higher level operators like "-fx" and "-composite" treat that data as representing 'alpha' data, for operation purposes. There is one another method of controlling the colorspace of the stored image data.

The "-set colorspace" (Added IM v6.4.3-7) will change just the in-memory 'colorspace' setting. That is it can convert a RGB image into a HSL image but without changing or modifying the actual pixel data that the image is using. The most typical use of this is when you are manually Combining Channel Data to set what is the final colorspace of the combined image.

So lets look at how we can manipulate color channels. Remember each channel is just an array of values. All the channels would then combine together to represent that actual color of each pixel within the image.

Seperating Channel Images

The easiest way separating out the individual color channels is to use the "-separate" operator to extract the current contents of each channel as a gray-scale image.

Notice how the red rose is prominent in the red channel image, while it is quite dark in the blue and green channels. On the other hand the green leaves are prominent in the green channel but not the others. The white near the bottom of the image is bright in all the channels.

In IM v5 and before "-channel" was not only a setting for later image operations but also on occasion an 'image operator' that converted the specified channel into a grey scale image. Very confusing! The IM v6 the "-separate", was created to 'separate' these two very different different tasks. The "-channel" option is only a setting that is used by later image operations, while "-separate" will extract the specified channels into separate gray-scale and fully opaque images.

As of IM v6.2.9-3, the "-separate" operator will let you separate multiple color channels according to the "-channel" setting. The number of items in the "-channel" setting will determine the number of images created (in RGBA order).

For example as the default "-channel" setting is 'RGB' the default action is to create three images, which I output below.

And here we use the "-colorspace" operator to convert the way IM is storing the color data of the image into a CMYK color representation. Then we extract the four color channels involved.

The last image (the 'Black' or 'K' channel) is especially interesting as it appears to be a negated gray-scale image of the original image. In reality it represents the amount of 'ink' a CMYK printer should deposit on the paper, reducing the amount of color needed by the other color channels.

Note that by default the "-channel" setting does not include the special Matte Transparency Channel of the image. If you want to always generate all channels that is present, you can use a "-channel ALL" channel setting, or use 'RGBA' or 'CMYKA' "-channel" setting.

In a similar way you can also extract the channels of other colorspaces. For example 'HSB' (Hue, Saturation, Brilliance), but which is also commonly known as HSV (Hue, Saturation, Value)...

Or a similar but not quite the same 'HSL' (Hue, Saturation, Lightness) representation. which uses a slightly different representation of how bright (its intensity) the image is.

Note that the 'Hue' channel image is a mottle of almost pure black and white colors. That is because a Hue is actually circular. That is both black and white in the above channel image are actually representations of a 'Red' Hue, and slight variations cause the hue to flip from one side of red (producing white) to the other (producing black). If this is a problem you can rotate the hue setting using the Modulate Operator so that red becomes represented by some other hue value.

Grayscale Channels from Colorspace Representations

You can extract specific channel values from colorspaces for special purposes. For example here we extract the images grayscale brightness or intensity from the rose image, using a number of different representations.

For the actual formulas see, the official reference to the "-colorspace" option.

Note that 'Gray' (also known as 'Intensity' or more exactly 'Luminance') and the 'Luma' of the YUV colorspace are equivalent. Similarly 'Brightness' of HSB colorspace, and the Negated 'blacK' channel of CMYK colorspace, are equivalent (and typically overly bright for grey-scale usage).

Note the 'Lightness*' channel from the L^*A^*B^* colorspace (not to be confused with 'Lightness' from HSL) is thought to be best match to the human visual perception, though it is not commonly used for generating grayscale images.

Generally when given a grayscale image, all the exampled colorspace channel images produce an exact match of the input grayscale image.

The exception to this is the 'Lightness*' ('R') channel image for a LAB colorspace. This does not produce an identical image to a input grayscale image.

Other Channel Separation Methods

One method is to copy one channel to all the other channels, to generate a grayscale gray-scale image, just as what the Separate Operator generates. A simple, but slow, method is to use the FX DIY Operator.

This is often regarded as the 'simplest' solution to understand, and has been used in other IM tutorials.

Other methods involve using a multitude of techniques to 'zero' out the unwanted channels. These are listed in Zeroing Color Channels below, and are usally a lot faster that using "-fx".

Combining RGB Channel Images

Once you have separated out all the image color channels, and processed them, you will also need to be able to rejoin the images back together again.

This can be done using the special list operator "-combine", which is basically exactly the reverse of "-separate". A user on the ImageMagick Mailing List wanted to be able to swap the red and blue channels of an image, this makes it easy, separate the channels, swap, and re-combine.

convert rose: -separate -swap 0,2 -combine rose_rb_swap.gif

Remember the default "-channel" setting is 'RGB', and can be used to define what images channel images are being joined together. If not all the channels being combined together are defined, the other channels are set using the color values from the current "-background" setting.

You should however note that both "-combine" and "-separate" will ignore the order in which channels are defined by the "-channel". Channels will always be processed and generated in the standard 'Red,Green,Blue,Matte' channel order, for each channel set in the "-channel" setting.

As such, even if you use a "-channel BR" setting or just "blue,red", the "-combine" operator will still expect the two images be red first then the blue. The green and alpha values (if images have transparency) will be set from the current "-background" setting values. For Example...

Combining non-RGB Channel Images

As of IM v6.4.3-7, you can also "-combine" channel images that represent other colorspaces, but you need to tell IM what colorspace the resulting image should be.

This is done by using the special "-set colorspace" operator. This basically changes the colorspace of an image in memory but without mapping the images pixel data, leaving it as is.

Once the image has been combined in the right colorspace you can use a normal "-colorspace" operator to map the pixel data back to normal RGB data.

convert separate_HSB_?.gif -set colorspace HSB -combine \ -colorspace RGB rose_HSB_combined.gif

This method also works for CMYK images, which is often difficult to handle due to the need for a fourth color channel.

convert separate_CMYK_?.gif -set colorspace CMYK -combine \ -colorspace RGB rose_CMYK_combined.gif

An alternative workaround (for earlier versions of IM) is to load one image and changing it so that it is in the right colorspace, After that the individual channel images can be loaded and Channel Copied into that pre-prepared image.

convert separate_HSB_0.gif -colorspace HSB \ separate_HSB_0.gif -compose CopyRed -composite \ separate_HSB_1.gif -compose CopyGreen -composite \ separate_HSB_2.gif -compose CopyBlue -composite \ -colorspace RGB rose_HSB_combined_alt.gif

Of course if you used "-set colorspace" operation, the data for the first channel will already be in place, as this does not change the actual pixel data, only the way the data is interpreted.

The last example will not work for 'CMYK' images, as the 'Black' channel image does not actually contain a black channel! As such "-compose CopyBlack" will fail to find valid data to copy. I regarded this as a bug, but is currently unlikely to be fixed.

Using other colorspaces can be useful. For example here I take the built-in rose image and want to negate the lightness channel (the last channel of HSL). When finished I re-combine to build a RGB image again.

convert rose: -colorspace HSL -separate \ \( +clone -negate \) +swap +delete \ -set colorspace HSL -combine \ -colorspace RGB rose_light_neg.gif

Note that the image still has the same colors, but the brightness (lightness) of the colors were reversed, producing a weird effect. You can replace the "-negate" with your own set of operations to adjust an images brightness levels.

However as "-negate" is itself a channel controlled operator we did not have to "-separate" out the lightness channel to negate it.

convert rose: -colorspace HSL \ -channel B -negate +channel \ -colorspace RGB rose_light_neg2.gif

As you can see this simplifies things, but it may not always be practical, for the effect you want to achieve.

Generating a Color Wheel

You can also use this technique of combining images to generate specific types of images which are hard to generate in other ways. For example here we generate perfect 'HSL' color wheel.

Zeroing Color Channels

Sometimes you have an image (RGB or some other colorspace) where you just want to clear or 'zero' one or two of the color channels but leave all the other channels as is.

For example, to make a greyscale image without using a RGB Gray-Scaling Techniques, you could 'zero' the Saturation channel ('G') in a HSL colorspace so as to make a gray scale image. The 'Hue' value has no meaning when saturation is zero, so you are left with a greyscale image.

The most direct technique, is often to use the Evaluate Operator to zero all the values in the unwanted channel...

convert rose: -colorspace HSL \ -channel G -evaluate set 0 +channel \ -colorspace RGB rose_grey.gif

However there are many not so obvious ways you can do this...

Can you think of another ways or zeroing (or maximizing) a color channel which I have not listed above? -- mail me

---

Color Specification

Colors in IM can be specified in many ways. The best guide on this is on the Official IM Website Color Names.

Colors by Name

Many colors have been given specific names, which make then easier to use. For example "RoyalBlue" is a very nice bright off blue color.

To the right is a image containing all the named colors, including those with numbers, that is available in ImageMagick. The colors were first sorted into 3 groups, Off-Whites, Mid-Tones, and Dark Colors, and then plotted in three separate HSL color-wheels, each with a different vertical offset. Pure white and black colors appear as there own separate spots at the very top and bottom of the chart, to form the extremes of the vertical range.

The script that generated it is "hsl_named_colors" and follows a technique looked at in Programmed Positioning of Layered Images.

Technically as I draw the HSL colors in the 3-dimensional form of a 'bi-cone' rather than a 'cylinder', the radius of each color spot has been set equal to the 'Chroma' of the color ('Saturation'/'Brightness'), rather than just its 'Saturation'. See Wikipeadia: HSL and HSV. To be more correct, Hexagonal Pyramids should also have be used instead of Cones, though that is harder to use when actually calculating positions.

As you can see you there a lot of color names associated with red to yellow and a smaller group in the cyan to green hues. With a similar cluster in off-white yellows and cyans. But there is little in the way of named off-green colors. Essentially there are some areas of the HSL color space that have very few named colors.

It can be difficult to find a specific named color to use. But by loading the image to the right in the IM "display" program you can use the middle mouse button to look at the ImageMagick color name for the specific color that has been plotted.

Special Color Names

There are a few special colors, whcih are used for special purposes within ImageMagick.

'None' or 'Transparent', is a fully transparent black color, and generally used to specify background transparency, such as when creating a Solid Color Canvas, or when using Image Layers.

'Opaque' is just an alias for 'Black', and as such is rarely used. It is typically used is when want to mean ANY opaque color, such as when doing Alpha Channel Processing.

Color Name Conflicts

Color Names can come from three different sources, SVG, X11, and XPM, and all are almost almost equivalent in there color naming. But where there is a conflict in the color assigned to a specific name the SVG (also HTML/CSS) color specification is used.

The biggest problem is the SVG color 'Green' (half bright green) which is is different to the X11 color 'Green' (pure RGB green). If you want a pure green, you are better off using the SVG color name 'Lime' which has no conflict.

Wikipedia has a excellent article on the color name conflicts, as well as a good table of the actual color names, in X11 color names. You may also like to look at the article Web Colors, which provide a set of nicely ordered table of some color ranges.

The most notable conflicts are in four specific colors. Here is a table of the known color name conflicts. Remember the SVG color is what IM will use bu default.

Conflict Color Name	SVG Result (IM default)		X11 Result for Name		X11 Equivelent Name		Alternative Color Name
Green		#008000		#00FF00				Lime
Maroon		#800000		#B03060		FireBrick
Purple		#FF00FF		#A020F0		Magenta
Gray		#7E7E7E		#BEBEBE				Grey

Notes about the above...

• The X11 'Grey' is a visual mid-gray color. It is also very close (but not exactly the same) as the X11 color 'Gray74' and SVG color 'Silver' ('gray(192)').

• The default (SVG) 'Gray' is very close to a perfect mathematical gray which is better specified using the color names 'Gray50' or 'gray(128)' (for 8-bit use).

• As all named colors are specified using 8-bit (0-255) values, none of them will generate a perfect 16-bit pure gray color!
  As such when a gray is needed for mathematical processing such as FFT DC Phase Edge Detection, Shade Images, Composition Lighting Effects, and Relative Displacement Maps you are much better off using the color formula 'gray(50%)' which does generate a perfect mathematic mid-tone gray at any color bit depth.

Caution is recommended when selecting a color for a specifc purpose.

Semi-Transparent Colors

You can directly specify semi-transparent colors directly in only two different ways.

The most common method of setting a semi-transparent color is to use a hex value.

For example here are some color specifications showing various levels of color transparency. I have displayed the generated color images on a background pattern so that you can see that pattern though the image transparency.

Before IM v6.3.0, the last set of hex digits contained the colors transparency in the form of a 'matte' value. That is a hexadecimal '00' represented 'opaque' and 'FF' was transparent. However after IM v6.3.0, this value was inverted so as to represent an 'alpha' transparency value, to bring IM in line with SVG standards and other graphics packages. In other words 'FF' now represented fully-opaque and '00' is fully transparent.

You can also specify colors using the special 'rgba()' color function. Where RGB values goes from 0 to 255, and the alpha channel is specified as a decimal fraction between 0.0 (transparent) to 1.0 (opaque).

Before IM version 6.2.7, the 'rgba()' also used a matte value for the alpha channel value. That is a value of 0 for fully opaque and 255 for fully-transparent. This was changed as defined by the "W3C CSS3 Color Module recommendation for specifying colors", as part of IM becoming more compliant with other image standards, particularly for WWW and SVG use.

It is currently impossible to directly specify a semi-transparent color by name, with an extra alpha value setting. However you can fudge it by generating that named color, then modifying the transparency of the image. You also have the added complication that you must Set the Alpha Channel, before you can actually set the colors transparency.

Yes this is a pain, and it would be nice if transparency could set as part of the color name specification. If you like to see this make a request on the IM Developers Forum.

It is also posible to draw a named fill color using MVG Drawing Settings, though you will need a transparent starting canvas for this to work correctly. For example...

convert -size 50x50 xc:none \ -draw "fill Tomato fill-opacity 0.5 rectangle 0,0 49,49" \ color_name_draw.png

Note that a fully-transparent colors while completely invisible, still has a color. However most IM operators recognise that any color that is fully-transparent, is the same and any other fully-transparent color. Because of this and the way the internal mathematics works, many operators will often replace a fully-transparent color with fully-transparent black, (also known as the special color 'none').

---

Replacing Colors in Images

ImageMagick naturally provides a number of options to replacing a specific and near match colors with another color. This is great when dealing with icons and 'bitmap' type images that contain very few colors, but tends to fail when dealing with images containing shades of colors or anti-aliasing edge pixels.

Basically you need to remember that colors are replaced by a single shade. So if you replace a set or neighbourhood of colors, all those colors are replaced by one specific single color and not by a matching range of colors. That is not to say it is impossible to do a shaded color replacement, just not simple to do at this time, without a lot of work.

Even so, GIF images does not allow the use of semi-transparency, so replacing colors in this way is a good method for controlling GIF background transparency (See GIFs on a Background Pattern for examples)

The other aspect is that while you can map all 'close colors' to a given colormap, using Pre-Defined Color Maps, you cannot currently do a global remapping of one set of colors to another completely different set. This is a short coming that may change in a future version of IM.

With that caveat, lets look at the ways IM does provide for the direct replacement of specific colors with another color.

Replace a Specific Color

The "-opaque" and "-transparent" operators are designed for replacing one color in an image with another.

For example to replace a 'blue' color with say 'white' you would use a command like this...

convert balloon.gif -fill white -opaque blue balloon_white.gif

Basically any color that was 'blue' has been replaced with the current "-fill" color.

However as of IM v6.2.7, this operator is limited by the "-channel" setting. As such, to convert a color (say blue) to transparency, you will need to specify a "-channel" to include the alpha channel to make colors transparent. You will also need to ensure the image has a 'matte' or alpha channel enabled, to hold the transparency information.

convert balloon.gif -alpha set -channel RGBA \ -fill none -opaque blue balloon_none.gif

Because replacing a color with transparency is such a common operation the above has its own special replace with transparency operator "-transparent".

convert balloon.gif -transparent blue balloon_trans.gif

As of IM version 6.3.7-10, the 'plus' versions of these operators inverts the color selection. That is, the colors that do NOT match the given color will be replaced. For example here I replace any color that is NOT pure-black, with white, leaving just the pure black borders of the image.

convert balloon.gif -fill white +opaque black balloon_borders.gif

This may not seem like much, but when you combine it with a Fuzz Factor (see below), this becomes a very powerful tool.

Before IM v6.3.7-10, the inverse operation required the use of some trickiness using image masks. Basically you replace the color you want to preserve with transparency, then "-colorize" all the other colors to the desired color to create an overlay mask. This is then overlaid on the original image to 'mask out' the colors that did not match! convert balloon.gif \ \( +clone -matte -transparent black \ -fill white -colorize 100% \) \ -composite balloon_mask_non-black.gif As you can see the 'plus' form of the operator simplified the 'not this color' replacement operation enormously.

For more advanced replacement techniques, I suggest you look at Background Removal.

Be warned that as all matching colors (especially 'fuzzy matched colors', see below) is replaced with a single uniform color, you will not get any anti-aliasing of the edges of the colored areas. And you will lose any an all shadow or other shading effects that may be present. This can have a seriously detrimental effect to the look off any non-simple non-cartoon like images. This type of color replacement is not designed with practical real world images in mind, but more for image masking effects. Caution is advised.

The "-opaque" color replacement cannot replace a color with a tiled pattern. It will only replace colors with another single specific color. However both the "-draw" and "-floodfill" color replacement methods can (see below).

Replace using a Color in the Image

You can also use Draw Color Replacement to recolor images based on colors present in the image itself, rather than a specific color.

convert present.gif -fill red -draw 'color 0,0 replace' present_blue.gif

Note that I never specified the color to be replaced, only the location of the color to be replaced. It is the color at that location that is used for 'matching' what areas is to be filled, regardless of what that color is.

You can see in the above example the problem with color replacement, the specific color may appear in other places that you intend, giving us a line of red pixels within the 'present' image above.

Transparency also presents no problem, though some internal parts of the image was also made transparent just as they became red in the above...

convert present.gif -matte -fill none \ -draw 'color 0,0 replace' present_none.gif

Note however that unlike "-opaque" and "-transparent" the Draw Color Replacement, does not let you invert the 'matching colors' to be replaced.

Draw also has a special Matte Replacement, where only the transparency of the fill color is replaced. That is, you can make all matching colors transparent, or semi-transparent, without actually changing the color of the pixel itself. With the appropriate file format of course.

convert present.gif -matte -fill '#00000080' \ -draw 'matte 0,0 replace' present_semi.png

This becomes much more useful when a Fuzz Factor is also specified.

The biggest advantage of using "-draw" is that you can also replace the color with a tile pattern. For example..

convert present.gif -tile pattern:right30 \ -draw 'color 0,0 replace' present_tile.gif

For more advanced replacement techniques, I suggest you look at Background Removal.

Floodfill Draw

The Draw Color methods also provide you with a simple method of replacing a color by 'floodfilling'. That is, rather than replacing ALL the matching colors within the image, you can select just the colors which are 'connected to' or 'attached' to the specified point in the image.

Again the specified point given sets the starting (or center) of the colors which are to be replaced.

convert present.gif -fill red -draw 'color 0,0 floodfill' present_fill.gif

Note that the red areas which was not 'attached' to the 0,0 pixel was note replaced.

For background replacing that can be a problem, but the solution is just as easy. Expand the image slightly so the floodfill can 'leak' into the image from all directions, then remove that extra space when finished.

convert present.gif -bordercolor white -border 1x1 \ -fill red -draw 'color 0,0 floodfill' \ -shave 1x1 present_bgnd.gif

Of course you can adjust what colors are 'matched' using the Fuzz Factor control setting below, which is especially important for JPEG images.

Floodfill Operator

The "-floodfill" operator was added to make floodfilling slightly easier, especially when you what to exactly specify the 'center' color for the Fuzz Factor color matching.

You can think of "-floodfill" as being more like the Opaque Operator with both a specific color, and a start (seed) point.

However be warned that if that seed point is not within a Fuzz Factor match of the color you are looking for then "-floodfill" does nothing. This can be regarded as the operators feature as well as its curse.

For example, add a border of known color to flood fill from edges...

convert present.gif -bordercolor white -border 1x1 \ -fill red -floodfill +0+0 white \ -shave 1x1 present_floodfill.gif

This will replace any color that is 'white' to 'red' that is directly part of the area surrounding the seed pixel starting at +0+0, whcih is guranteed to be 'white' due to the added border.

You can also floodfill with a tile pattern.

convert present.gif -bordercolor white -border 1x1 \ -tile pattern:left30 -floodfill +0+0 white \ -shave 1x1 present_pattern.gif

For more advanced replacement techniques, I suggest you look at Background Removal.

Fuzz Factor - Matching Similar/Multiple Colors

The overall results of just selecting a single color to replace, as shown in the previous examples is usually not very nice. The edges or areas of solid colors generally have a mix of colors at the edge, due to anti-aliasing (See Anti-Aliasing for more information). As such you should avoid direct color replace if possible.

For example here I take what looks like a simple black and white 'cow' and try to make it a red cow.

As you can see only the center parts of the 'black' areas actually became red. That is because, while the image appears to be black and white it is really a gray-scale image with almost all the edges various shades of gray. That is, they are not exactly pure-black in color.

The fuzz factor, ("-fuzz") represents a 'similarity' match in multi-dimensional spherical distance between colors, using whatever color space the image is using.

Well okay lets try that in plain English. You have a specific color. Another color will be treated as being same as the color being looked for, if the difference between these colors is less than the fuzz factor setting. The larger the 'fuzz factor' and more 'near' colors will match and be replaced.

So lets try that on our cow image so as to convert not only pure-black but also near-black colors to red.

As you can see we now replaced all the 'dark' pixels of the image to red. But the result is still very bad, with a grayish tinge to the edge, and strong Aliasing effects. Direct color replacement is not a good solution for this image, even though you can make it work using a large 'fuzz factor' . See the examples in Level adjustments by Color for the ideal solution for this image.

This problem is even worse for images where you are trying to replace a background color with transparency. You basically end up with a 'halo' around the object on that background color. This is very difficult to solve, and problems like this are looked at in detail in Background Removal.

What operations use fuzz factor

The "-fuzz" operator effects just about any operator which compares specific colors within an image. This includes: "-opaque", "-transparent", "-floodfill", "-trim", "-deconstruct", "-draw 'color'", "-draw 'matte'", and probably others. It also effects GIF "-layers OptimizeTransparency", and "-compose ChangeMask" handling.

It also effects the results of "compare" and specifically the "-metric AE" or Absolute Error Pixel Count.

Fuzz Factor Distance

The "-fuzz" setting is actually a form of color 'distance' setting. Any color that is within the given distance of the color being looked for, will match that color, even though it is not an exact match.

A value of '200' represents a distance of 200 color units in the current color depth of the IM being used. For a IM Q16 (16 bit quality for color store) this is quite small, for a IM Q8 this is VERY large, and will cause a lot of colors to match each other.

Here for example I change all the colors that are within 30,000 color units (for IM Q16) of 'blue' to white. With my Q16 ImageMagick programs, that represents approximately the distance from 'blue to 'navy' (half dark blue), convert colorwheel.png -fuzz 30000 -fill white -opaque blue opaque_blue.jpg

To make this easier to understand here I invert the matched colors turning the unmatched colors to white. convert colorwheel.png \ -fuzz 30000 -fill white +opaque blue \ opaque_blue_not.png

If your IM is older than version 6.3.7-10 when the 'plus' form of the "-opaque" operator was added, you can use this masking method to invert the result of the color match... convert colorwheel.png \ \( +clone -fuzz 30000 -transparent blue \ -fill white -colorize 100% \) \ -composite opaque_blue_inv.png

Or this method that limits all modifications to just the 'alpha channel', so that all the original colors, are left as is. That is, you create a negated mask from the color selection, so as to make all non-selected colors fully-transparent. They remain present, just transparent! convert colorwheel.png -fuzz 30000 -transparent blue \ -channel A -negate +channel opaque_blue_inv_alpha.png

An advantage of these methods is that you can expand them to generate a 'not multiple colors' technique. All that you need to do is add more colors to the list being made transparent, before negating the mask. convert colorwheel.png \ -fuzz 25000 -transparent blue -transparent red -transparent lime \ -channel A -negate +channel \ -background white -flatten opaque_multi_inv.png

As a matter of interest, in a IM with a Q8 compilation setting, a "-fuzz" factor of 256 (28) will make the colors 'black' and 'blue' the same. For a IM with a Q16 setting this number is 65536 (216). To make 'blue' and 'red' colors match this number must be multiplied by the square root of 2, or 362 for IM Q8, and with 92682 for IM Q16. Finally to make all colors match (eg colors 'black' and 'white') you will need to multiply by the square root of 3. In other words, a fuzz factor setting of 444 for IM Q8 and 113512 for IM Q16.

As you can see from the above formulas, direct color distances is definitely not a nice way of setting the fuzz factor to use, as it is also dependant on exactly what compile time Quality Setting is used.

Setting the "-fuzz" factor as a percentage, makes its use a lot simpler. In this case '100%' represents a large enough fuzz factor to cover all colors. That is, it represents the color distance from 'black' to 'white', across the 3 dimensional diagonal of the RGB color cube.

To demonstrate lets change 90% of all the colors closest to 'white', white. This should result in only the last 10% colors near 'black' on the image, as black is on the opposite side of the RGB color cube. convert colorwheel.png -fuzz 90% -fill white -opaque white opaque_w90.jpg

Note that as the 90% represents a sphere of colors around 'white' in RGB color space. This however is not the same as replacing the colors that are not within a 10% sphere of black. convert colorwheel.png -fuzz 10% -fill white +opaque black opaque_k10.jpg

As you can see 10% sphere of colors near the black is much more uniform, than selecting a 90% sphere of the colors around white.

A "-fuzz" factor of 100%, equates to the RGB color cube distance from 'black' to 'white'. From this we can calculate that a percentage of about 57.7% is the distance between 'black' and 'blue', and 81.6% is the distance from 'blue' to 'red' or from either of those colors to 'white'. In summary, anything larger than about 25%, (just short of the RGB distance from 'blue' to 'navy blue' represents a very large color change.

To demonstrate the color distances more, lets use a progressively larger fuzz factor percentage around the blue colors...

From this you can clearly see that it isn't 'black', or 'white' that is the most distant color from 'blue', but that it is actually 'yellow' that is most distant within RGB color space.

Also note that a 81% color difference will just miss matching a pure 'red' color, however while pure red does not match almost all of the other reds do. That is again due the to 'spherical' nature of the color matching. The moral is that you are probably better off either using multiple small "-fuzz" factored matches or a smaller 'inverted match', than a single large value.

Here we compare the colors in the image with another color, the 'perfect gray' color, changing similar colors to that grey color, at various 'fuzz factors'.

As you can see colors in the colorwheel image only just start to match at a fuzz factor of 30%, and slowly increase until at 45% all but the most extreme colors have disappeared. At 51% all the colors in the image has matched.

What you are seeing is the result of the way RGB colors are arranged into a cube in 3-dimensional space. The 'color wheel' image however only contains 'fully saturated colors', which basically means all the extreme colors that are located on the outside faces of that color cube.

A perfect gray is however located in the center of the cube, quite distant from all the 'saturated colors' on the outside of the cube. As such it is not until you reach a large fuzz factor of 28%, that the color in the middle of the cube face faces start to match.

As the fuzz factor gets larger more and more colors will match until only the colors at the extreme corners of the color cube remain. At around 50% even those corner colors will start to match, and so at 51% every opaque color will have matched.

Fuzz Factor and Transparent colors

Using a "-fuzz" factor becomes more complicated when matching involves transparent and semi-transparent colors.

For example here I create a gradient between black and white, across the image, but then add a transparent gradient vertically. I then do a fuzzy color match for a perfect gray color (that is 50% gray). In later images I make the color being match more transparent until it is fully-transparent, however the Fuzz Factor remains a constant 20%.

Note the use of "-channel RGBA" in the above is not for color matching, but for specifying the color channels to be 'filled'. That is without it, the above will still match the same colors, but gray 'fill' will remain semi-transparent, and not be set to a opaque gray color.

If you want to match all colors regardless of their transparency, then you will need to Turn Off Transparent Channel of the image, at least temporarilly. You can turn it back on again afterward, though your fill color will again have the same transparency as the original color.

In the first image matching with a fully-opaque gray color (alpha='1.0') you get a very spherical match of all the near opaque gray colors. However as the color being matched gets more semi-transparent, the number of matching semi-transparent colors that match will seem to become larger, until a fully-transparent grey will match any near-transparent color.

What is happening is that as transparency increases, the distance between the semi-transparent colors decreases. The more transparent two colors are the closer the colors will be, compared to their opaque counterparts. When both colors are fully transparent, the two colors will be regarded as a perfect, or '0' distance, match.

The other thing to notice is that (as of IM v6.6.6-4) the distance from a fully-transparent color (grey or otherwise) is purely a function of the colors transparency (alpha value). The last image in the above matched all pixels that was within 20% of being fully-transparent, regardless of actual color.

This also means that a large Fuzz Factor with a fully-transparent color (like 'none'), can be used to match all, or almost-all semi-transparent colors. For example... convert trans_gradient.png -channel RGBA \ -fuzz 95% -fill Gray50 -opaque None \ -alpha off fuzz_trans.jpg

Notice that only the top 5% of the near opaque colors in the above did not match, while all the other semi-transparent colors, was turned grey. The final "-alpha off" removes the last bit of semi-transparency from the image. Because of this the "-channel RGBA" setting is not actually needed, but is recommended for completeness.

This example is essentially equivalent to a threshold of the alpha channel, followed by a gray color underlay (to make transparent colors grey)

Before IM v6.6.6-4 fuzz color matching did not match fully-transparent with opaque colors equally. In fact Black was much closer match than White. As such the last example will fail. See Fuzz Distance and Transparent Colors Bug for more details.

Worse still before IM v6.2.6-2 fuzz color matching did not regard all fully-transparent colors as being the same color. That is fully-transparent black (also known as 'None') was not the same as fully-transparent white (or color '#FFF0'), even though they are both fully-transparent.

---

Color maths (get the average of two or more colors)....

  Example Averaging two colors... Say '#000000'  and  '#DDDDDD'

  Generally the colors are added to images, and the result output as a
  single pixel 'txt:-' image, which which the color can be extracted.

  * use -resize to merge the colors

      convert -size 2x1 xc:'#000000' -fill '#DDDDDD' \
              -draw 'point 0,0'  -resize 1x1  txt:-

  * Use -average on them!

      convert -size 1x1 xc:'#000000' xc:'#DDDDDD' \
              -average  txt:-

    Or for a lot of colors you can use the 'Box' resize filter
      convert rose: -filter Box -resize 1x1\! txt:
      # ImageMagick pixel enumeration: 1,1,255,RGB
      0,0: (145, 89, 80) #915950

  * Use -fx to apply whatever formula you want

      convert -size 1x1 xc:'#000000' xc:'#DDDDDD' \
              -fx '(u+v)/2'  txt:-

  With a ImageMagick API the results can be more directly retrieved from the
  image.